曲げ挙動は構造物の設計施工や保全の検討に際し、最も主要な事象であり、その力学的な基本は「曲げモーメント」と「曲度(Curvature)」との関係で構成されます。したがって「曲度」は構造工学の中で最も基本的な事柄であるにもかかわらずその名称は語彙的に矛盾のある「曲率」なる用語が現在でも一般に用いられています。本稿のその1、その2、およびその3で「曲率」を「曲度」に変更する必要性を論じましたので、本稿（その4、最終稿）では英語のCurvature を「曲度」の用語で記述します。語彙的な矛盾とは曲線半径の逆数、すなわち、「1/曲線半径」の次元を持ち無次元でないにも拘らず「率」という語尾を持つことです。激しい文明の競争の中でLiteracy（文字表現能力）の論理性を正すことは極めて重要と考えられます。

　PC構造（プレストレストコンクリート構造）の特徴は、プレストレスにより全断面が圧縮状態で断面力に抵抗するので弾性体として機能を発揮し、曲げモーメントと曲度の関係が直線関係となることで、復元性、強靭な弾性体として供用性が優れていることです。そのうえ、大きな曲げモーメントが作用して断面がディコンプレッション（離圧）状態以降になっても除荷すればPC鋼材の緊張力によって復元性が確保される非線形弾性の性能があるのです。この非線形弾性の特質がPC構造の優れた耐震性の原点となり得ます。本稿ではその非線形弾性特性を定量的に表現するPC構造固有の「曲げモーメント」-「曲度」の関係およびそれに立脚した曲げ性能について柱に鉛直方向のプレストレスを導入したPC柱を対象として述べます。

(1) 非線形弾性特性の無次元化

　ここでは鉛直方向にプレストレスを導入したPC柱およびPC橋脚が曲げモーメントを受ける状態を対象とし、断面は長方形断面とします。また、耐震性の検討が主であることから正負繰り返し荷重が作用するのでコンクリートの引張抵抗は無視し、PC鋼材は弾性範囲として常に一定の緊張力を保持することとします。

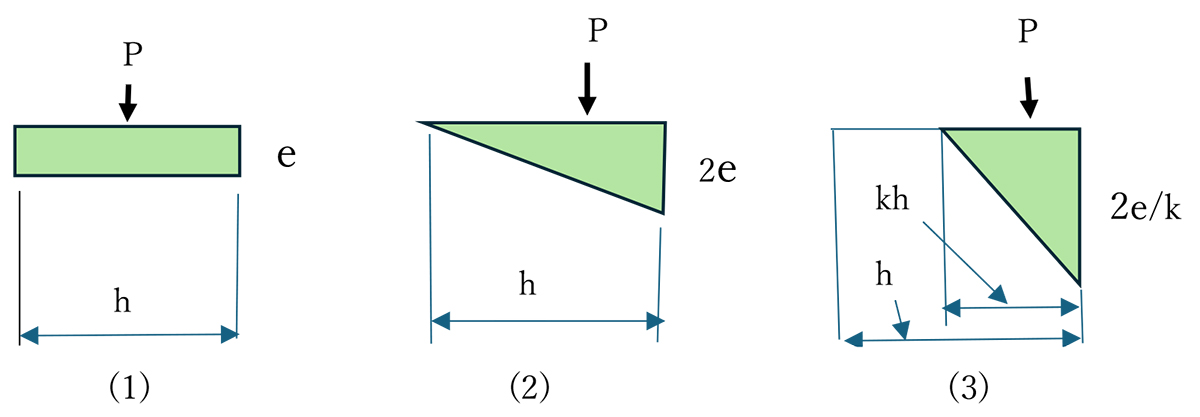
図-1　曲げモーメントの変化によりプレストレス力の位置とひずみ分布が変化する状態

　図-1に断面の中心にプレストレス力Pが作用した状態で曲げモーメントが増加し、断面のひずみ分布が変化する状況を示します。図-1(1)は曲げモーメントがゼロの時でひずみ勾配はゼロです。

　図-1(2)は片側の外縁のひずみがゼロのディコンプレッション（離圧）状態の時であって圧縮側のひずみは図-1(1)の場合の2倍の2eになり、ひずみ勾配ФはФ=2e/h です。ここでhは断面の高さ（両外縁間の距離）です。この時の曲げモーメントMはPが偏心軸力として移動する距離がh/6なので M=Ph/6 です。この時（離圧時）のФおよびMを基準値とし、以降の状態の時はその比率として無次元化してこれらの値をそれぞれφおよびmとします。

　図-1(3)は曲げモーメントが増加してひずみがゼロの位置が圧縮縁からkhの位置にあるときでk=1/2では断面中心にある場合です。この時のひずみ勾配ФはФ=4e/(h/2)=8e/h で離圧時の４倍で無次元のφはφ=4です。これに対応する曲げモーメントMはM=P(h/2-h/6) =Ph/3 で離圧時の2倍であり、無次元のmは、m=2です。すなわち、無次元の曲げモーメントmとひずみ勾配φの関係は点(0,0),(1,1)および点(4,2)を通る線で表示できます。同様にしてφが9の時のmは7/3=2.333 となります。ひずみ勾配は本稿（その1、その2、その3）で詳述したように「曲度」のことです。

　これらの関係を無次元の直交座標で示したものが図-2です。この図は非線形弾性特性を持つPC柱の「曲げモーメント」と「曲度」の無次元の関係を普遍的に折れ線で示すものです。

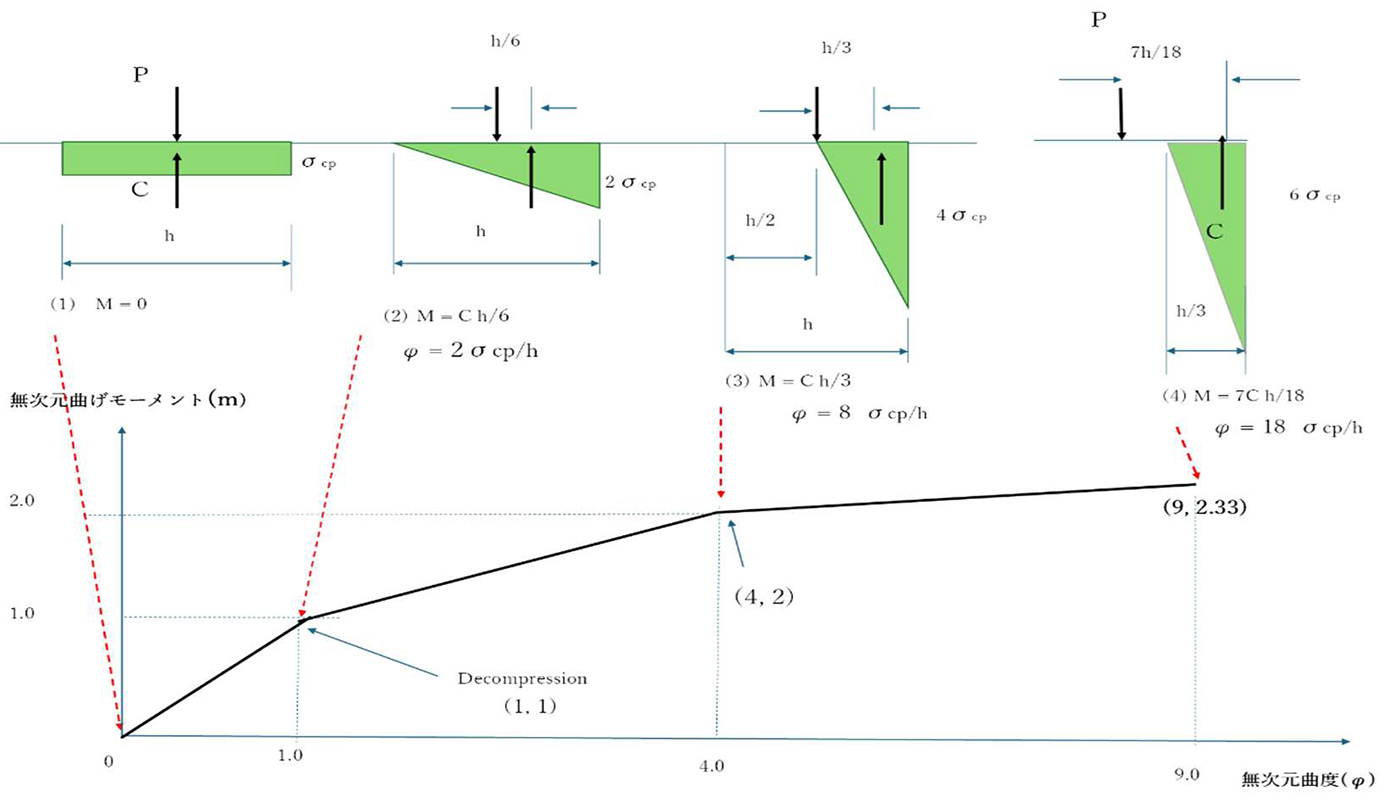
図-2 無次元化した曲げモーメントと曲度の関係

　(2) 非線形弾性特性の無次元での定式化

　図-1(3)を用いてPC柱の曲げモーメント-曲度の関係を無次元的に定式化することを考えます。断面のひずみがゼロの位置を圧縮縁からkhとすればプレストレス力Pが一定であり、ひずみ分布を表す3角形の面積が一定ですので圧縮縁のひずみは2e/kとなります。したがってひずみ勾配、すなわち、曲度ФはФ=(2e/k)/(kh)=2e/(h k²)で、この時の曲げモーメントMはM=P(h/2–kh/3)です。これらの値を離圧（ディコンプレッション）時の値(k=1の時)で割って無次元化するとφ=1/k²、すなわち、 k=1/φ^0.5なので、m= P(h/2–kh/3)/(Ph/6)=3–2k=3–2/φ^0.5 となります。
以上により、mとφとの関係は、式(1)として定式化されたのです。

　m=3–2/φ^0.5 　　　　　　　(1)

　ここで、mおよびφは作用曲げモーメントMおよび曲度Фをそれぞれ離圧時の値で割って無次元化したものです。

　当然のことながら図-2の点(1,1),(4,2)および(9, 7/3)は式(1)を満足します。また、φ=2の時はm=3-√2=1.586です。

　PC部材の曲げモーメントと曲度の関係は正規化された式(1)で表されます。この式は離圧（ディコンプレッション）以降の無次元化された曲げモーメントmと曲度φとの関係を表す普遍的な理論式であり著者らにより見出されました¹⁾。なお、この簡潔な普遍式は、力のつり合いとひずみ分布の幾何学的な形状から前述のように明解に誘導することができます。

　一方、荷重と変位との関係は、非線形の式(1)を用い数値解析によって精度よく求めることができます。すなわち、PC柱の上端に水平荷重Pが作用するときの柱頭の変位δは周知のように式(2)を数値計算することによって求められます。

δ = ʃ Mo Ф dx 　　　　　　(2)

　ここで、 M0 :柱頭にVirtual Load(仮想荷重)1.0の作用による曲げモーメント、Ф:曲度

　構造計算上では荷重と変位の関係の実用的なモデル化が必要です。PC構造の無次元での荷重pと変位δの関係については式(1)の非線形弾性特性が支配的であるので式(3)を設定して適切な指数nを求めることとしました。

p=3–2/δⁿ 　　　　　　　(3)

　式(3)の指数nは、 参考文献²⁾に詳述されたように式(2)の数値計算による積分値として求めたδ=4.959、 p = 2.4を用いて同定すると n = 0.7519が得られ²⁾、また,同様にp = 2.5のときのδ=6.14を用いるとn = 0.7468 が得られたので n = 0.75 として式(4)を定めることができました。

p=3–2 /δ^0.75 　　　　　(4)

　地震時の応答計算に有用なPC柱の無次元化された正負の荷重-変位の関係³⁾を式(5)に新たに示します⁴⁾。

 p=aδ+sgn(δ)(3 – 2/|δ|^0.75)(1 – a)　　　 (5)

　ここで、 p:荷重、δ:変位、sgn:符号関数、|δ|>1.58: a=0、|δ|≦1.58: a=1

　以上に述べた定式化は次元を持つ曲げモーメントや曲度などを、離圧(ディコンプレッション)時を基準として無次元に正規化したものであり、この手法によりPC構造固有の非線形弾性特性を普遍的、実用的に表現することが可能となったのです。

　図-3に式(5)として求められた正負の非線形弾性特性を持つPC柱の無次元化した荷重と変位の関係を示します。

　PC構造の地震応答解析を行うにあたり、式(5)による数値計算を行うことが合理的な耐震設計の手段になり得ます。また、適切な等価粘性減衰係数を用いて式(5)に対応する線形の微分方程式による応答計算をすることが可能です。この場合、靭性率を4.0として等価粘性減衰比を10%および等価ばね定数を離圧前の57%とすることを提案できます。

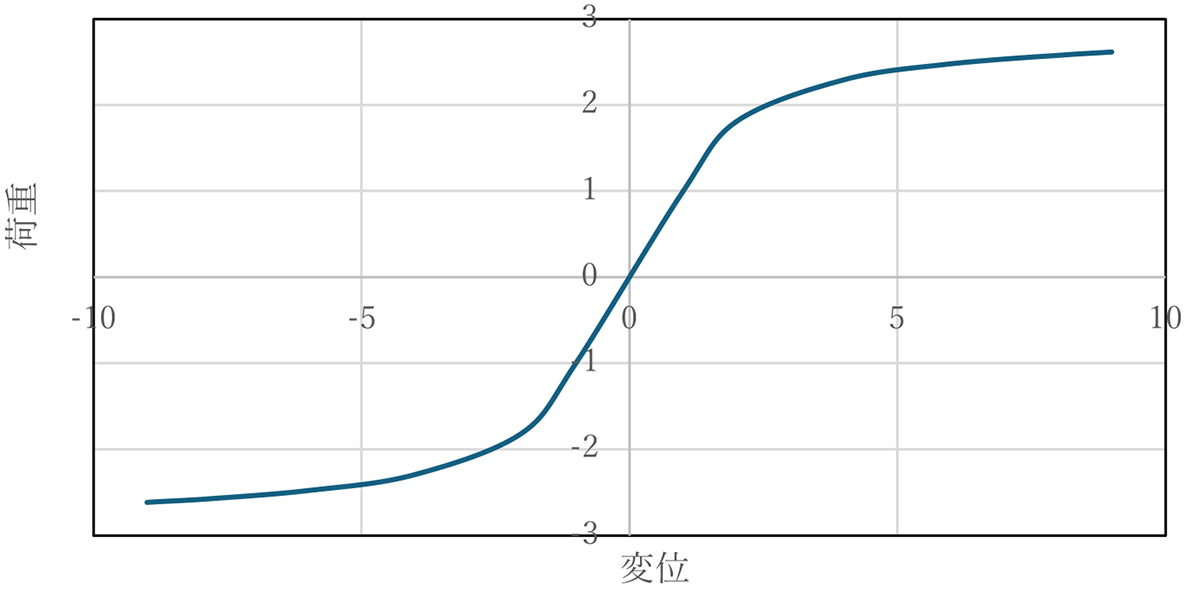
図-3 式(5)による無次元化した非線形弾性の荷重と変位

　1) 長さの逆数の次元を持つ「曲率」という用語を「曲度」に変更する提案を基本として曲度に関する基本的な考察を行い、構造工学の観点からPC構造固有の曲げ挙動について述べました。

　2) PC構造の優れた耐震性は離圧(ディコンプレッション)以降の曲度の非線形弾性特性に依存するものであり、次元を持つ曲度と曲げモーメントの関係を,離圧(ディコンプレッション)時を基準として無次元に正規化することによって普遍的にPC構造の非線形な弾性挙動を把握できる曲げモーメント-曲度の式、および荷重-変位の式を示しました。

　3) 断面のプレストレスが曲げモーメントの作用によって外縁でゼロになる状態に対し、ディコンプレッション(Decompression)という用語が一般に用いられていますが本稿ではこれを「離圧」と称する日本語で表現しました。

　4) 水平な線が曲がる時、その形状を２回微分した値が「曲線半径の逆数」になることが数学的に得られます。一方、力学的には曲げを受ける梁断面の「ひずみ勾配」、すなわち、「曲度」は梁の変形における「曲げ半径の逆数」に一致します。したがって、「曲度」は曲げ変形に関して数学と力学とを結び付ける鍵語（キーワード、Keyword）なのです。

付記
“「曲げ性能」は供用性、安全性、耐震性の基本”と題して４回にわたり論じました。本稿は最終回です。「曲度」に関連し、「キーワード」を日本語で「鍵語」と表現しました。

参考文献
1) 池田尚治, 黒沢亮平： PC構造の変形特性の定式化と耐震設計への適用,プレストレストコンクリート,第64巻1号,研究報告,pp.53-60, 2022.1
2) 池田尚治, 黒沢亮平: PC構造における非線形弾性変形の定式化および耐震限界状態の研究, 第30回 PCの発展に関するシンポジウム論文集,pp.53-58, 2021.10
3) 池田尚治, 黒沢亮平, 平井圭：免震機能を持つPC柱の耐震性能に関する研究,第32回 PCの発展に関するシンポジウム論文集,pp.113-118, 2023.10
4) 池田尚治, 黒沢亮平, 平井圭：曲げ変形の基礎的考察とPC構造固有の曲げ挙動,第34回 PCの発展に関するシンポジウム論文集,pp.377-380, 2025.10