「曲げ性能」は供用性、安全性、耐震性の基本
1.はじめに
曲げ変形および曲げ挙動は構造工学にとって最も根幹的な事象であり空間を形成しその安全性、耐震性と供用性の確保のために構造設計での主要な検証事項です。その基本となる力学の論理は「曲げモーメント」と「曲率」の関係であると認識されています。しかしながら英語のCurvature の日本語として「曲率」という用語が定着しています。曲率は長さの次元を持つにもかかわらず「率」という無次元の漢字表現では語幹的に不合理と思われます。そのため事象の正しい認識が困難だと考えられます。以前は力と長さの次元を持つにもかかわらず「弾性率」、「ヤング率」という用語が広く用いられていましたが現在では「弾性係数」、「ヤング係数」という用語に変わっています。そこで語幹的に不適切と思われる「曲率」を「曲度」に変更をすることを提案したいのです。
なお、筆者は日本コンクリート工学会の会誌2021年2月号に資料として曲率の持つ2面性について述べましたが、本稿ではその後も考察を進め、新しい用語を提案したいと思います1)。
2.直線の折れ曲がり
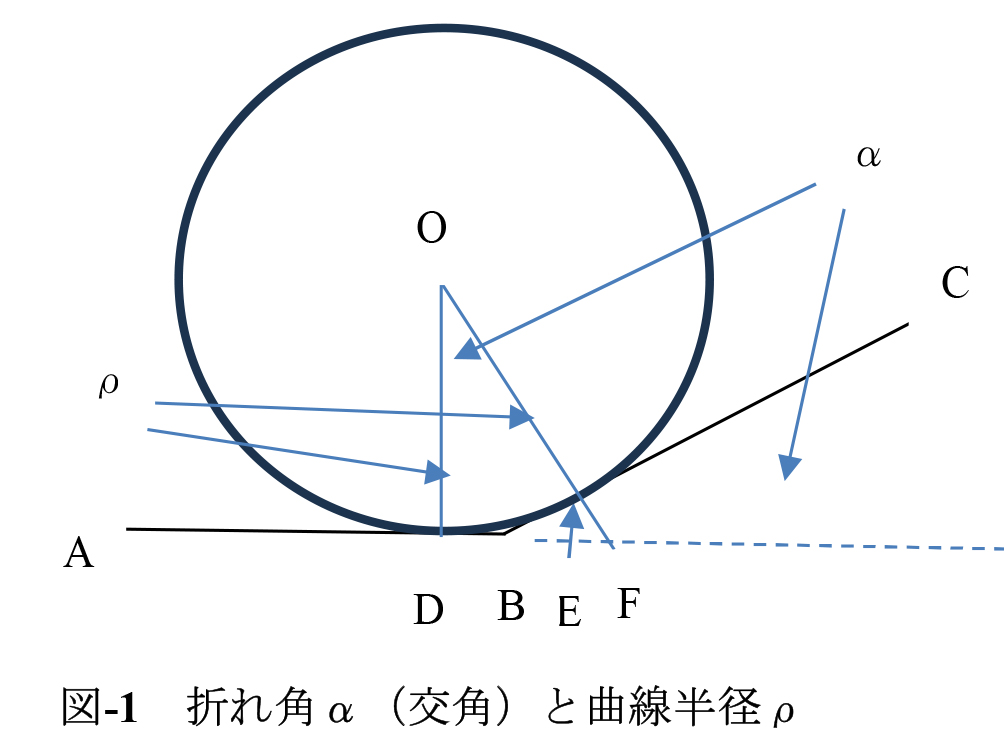
曲線について考える場合には先ず直線の折れ曲がりについて把握することが肝心です。そこで、直線がαの角度で折れ曲がる状態を考えます。図-1に示すように直線ABと直線BCを考え、2直線の折れ角(交角)をαとします。また、両直線に接する円を考え、D点およびE点でそれぞれの直線に接するとします。点Oは円の中心であり、その半径をρとします。
直線ABおよびBCに関し、直線DO およびEOは、それぞれ直線ABおよび直線BCに直交しているので角DOEは折れ角(交角)αに等しいことがわかります。あるいは、三角形DOF,EBFは点Fでの角が共通な直角三角形なので相似であり角DOEは折れ角αと等しいことが納得できます。また、折れ角αを定めれば三角形DOEは2直線に内接する円の半径が変化しても常に相似です。
円弧DE、半径ρおよび折れ角αの関係は式(1)で示され,これを変形して式(2)が得られます。
 円弧 DE = ρ α (1)
円弧 DE = ρ α (1)
1/ρ =α/DE =φ (2)
φは「曲率」と呼ばれるものであり長さの逆数の次元を持っています。これを曲率という無次元
の意味を持つ漢字で表現することは適切でないと思われます。角度を円弧の長さで除しており曲がり
程度を表しているので、1/ρ=φを「曲率」に変えて「曲度」と呼ぶことにしたいのです。
3.曲線半径と歪み勾配
図-2(1)に長さL の梁部分が曲げによって変形し、上縁がΔLだけ圧縮される場合の曲線半径ρ、断面の軸回転の角度β、中立軸から上縁までの距離aの関係を示します。同様にして図-2(2)には図-2(1)の横軸を梁の長さLで割った状態を示します。すなわち、L部分は無次元の1.0、ΔLはΔL /L = εとなり、また、単位長さ当たりの角変化度(=曲度)はγとなり、一方、縦軸はそのまま長さρおよびaを表す図を示します。なお、ここではコンクリート梁の断面の圧縮側を対象としています。
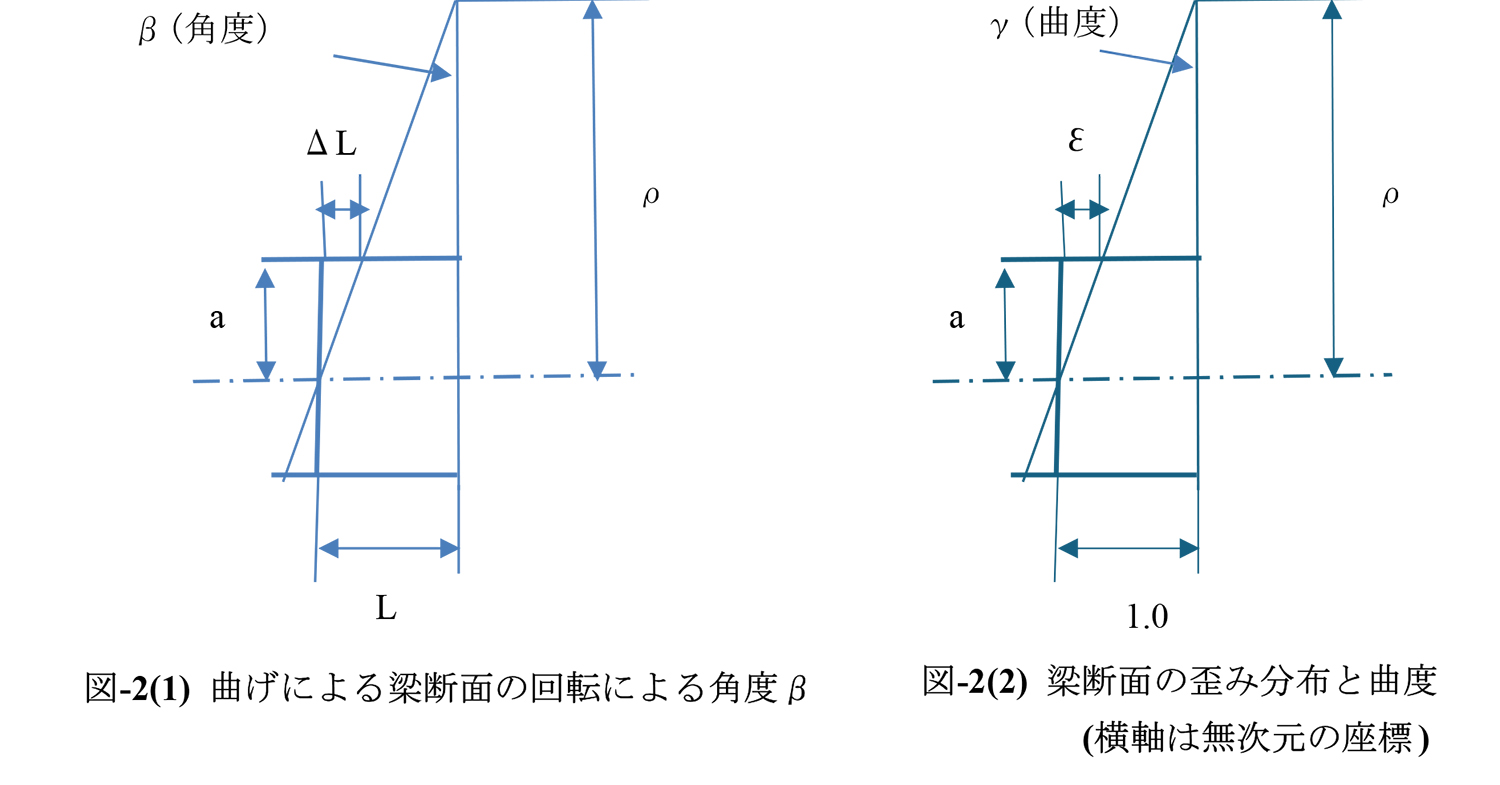
図-2(1)で明らかなように、ρを一定値とすればLが如何に変化してもΔL/Lの値は一定であり図-2(2)が得られます。図-2(2)から明らかなように曲度である1/ρは3角形の相似の関係からε/a と等しいので断面の歪み勾配であるγ(曲度)は、式(2)の曲度φと等値なのです。歪み勾配は縦軸に長さ、横軸に無次元の歪み値を表すデカルト座標(Cartesian coordinate)において視覚的に図示されていますが横軸は無次元の世界でγは我々の存在する平面上での角度ではありません。また、図-2(1)の角度βは図-1の折れ角αに対応します。
4.梁断面の曲げ形状
梁断面の縁応力度を求める式はよく知られているように式(3)で表されます。この式は平面保持の仮定を基に曲げモーメントMのつり合い条件から簡単に誘導することができます。ここでのa は断面上縁と中立軸との距離、Iは断面2次モーメントです。
σ = (M/I) a (3)
両辺をヤング係数Eで割ると歪みが求められ、これをさらにaで割れば次式が得られます。
е/a = M/(EI) (4)
е/a は歪み勾配、すなわち曲度φであり、1/ρ です。
したがって、曲げモーメントと曲度との関係は式(5)で表されます。
φ = M /(EI) (5)
曲線を形として理解するには曲線半径が適切であって曲度では形象的には表現できないのであり、一方、断面の歪み分布や歪み勾配は曲線半径よりも曲度の方が適切なのです。つまり、形象の世界を曲度で表現することは感覚的に理解することが困難なのであり、これに対して断面の変形を考える場合には歪み勾配、すなわち、曲度を用いることが簡潔に表現できるのです。
5. 折れ角と曲度
折れ角と曲度あるいは曲線半径とは独立事項です。
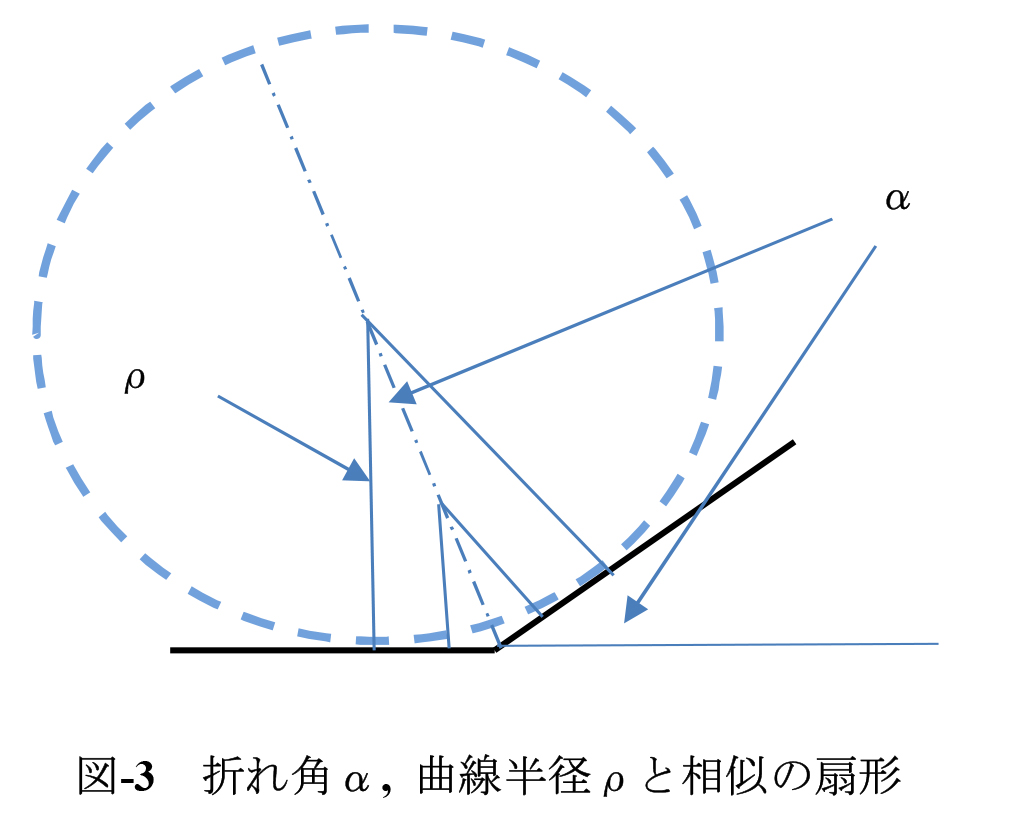 曲がりの状態を表現するには折れ角と曲線半径の両方が必要なのです。図―3に折れ角αと曲線半径ρの関係を示します。この図から明らかなように視覚的に曲線を定量的に把握するには折れ角と曲線半径あるいは曲線の長さによることが適切であり、曲度の概念は不要です。
曲がりの状態を表現するには折れ角と曲線半径の両方が必要なのです。図―3に折れ角αと曲線半径ρの関係を示します。この図から明らかなように視覚的に曲線を定量的に把握するには折れ角と曲線半径あるいは曲線の長さによることが適切であり、曲度の概念は不要です。
折れ角は曲線の始点および終点における角度の変化を表すもので曲がりの形態を示す重要な指標です。図―3で明瞭に示されているように折れ角が一定ならば曲線半径と円弧で形成される扇形は常に相似です。
扇形が大きくなればカーブは緩くなり、小さくなればカーブは鋭くなります。扇形部分は2つの直線を円曲線によってスムーズに繋ぐのです。
図―3で曲線半径ρを一定にして角度αを小さくし、円周に沿って折れ線の数を増やせば折れ線の集合は円周に近付き、限りなく小さくすれば円周と一致します。この場合、円弧の長さをdx,折れ角をdθとすれば ρ(dθ)=(dx)ですので(dθ)/(dx)=1/ρ=φであり、線の角変化の度合いが曲度なのです。
ついでながら線のx軸に対する角度をθとすればθ=(dy)/(dx)ですので(dθ)/(dx)=(d2y)/(dx2)であり、式(5)と組みあわせて構造力学の基本である式(6)が得られます。数学と力学の合体です。
(d2y)/(dx2) = M/(EI) (6)
6.まとめ
現在広く用いられている「曲率」という用語は長さの逆数の次元を持つにもかかわらず「率」という無次元の漢字表現となっていて語幹的に不適切と思われます。英語では「Curvature」であり、これを「曲率」から「曲度」に変更する提案をするために曲線に関する基本的な考察を行いました。
曲度は長さの逆数の次元を持つので感覚的には認識が難しいと思います。これを理解するには例え話が役に立ちます。5個のお菓子を5で割れば1個です。しかし5人で割れば1個/人であって1個のお菓子の下に1人の人間が存在するのです。5で割った1個のお菓子を頂戴するのは問題ありませんが、5人で割った1個/人 のお菓子に他人が手を出せば喧嘩になります。次元の有無と意義とを正しく認識することは重要なのです。
次回は「曲がり」の無次元化についての考察です。
参考文献
1) 池田尚治、曲率の次元に関する考察、コンクリート工学 2021年2月号、資料、pp.194-195,Vol.59,No.2,2021.2,日本コンクリート工学会














 お問い合わせはこちら
お問い合わせはこちら