線は長さを持つが太さを持ちません。したがって形象的には存在しないものであり、論理上の概念での表現なのです。点も全く同様であって大きさを持たないことと同じです。なお、数字も同様であって本来は人間が１人、２人などのように単位を持つものが自然状態での概念であるので、数字のみでは無次元の抽象値です。数学者によれば代数学は数字の抽象値の概念の誕生により発達したとのことです。

　曲げに関する数式の誘導についてはすでに本稿の「その１」で概要を述べましたが、ここでは線に太さを持たせて数式の誘導することについて改めて詳しく述べます。線の曲がりの形状は曲線半径ρによって一義的に定められます。この場合の線は太さを持たなくてよいのです。線が２次元座標でx軸に対して角度θであるときθ＝dy/dx、その変化はdθ/dx =d2y/dx2であり、図‐３に示すようにρdθ=dx なので式（１）が成立します。

d²y/dx²=1/ρ 　　　　　 (1)

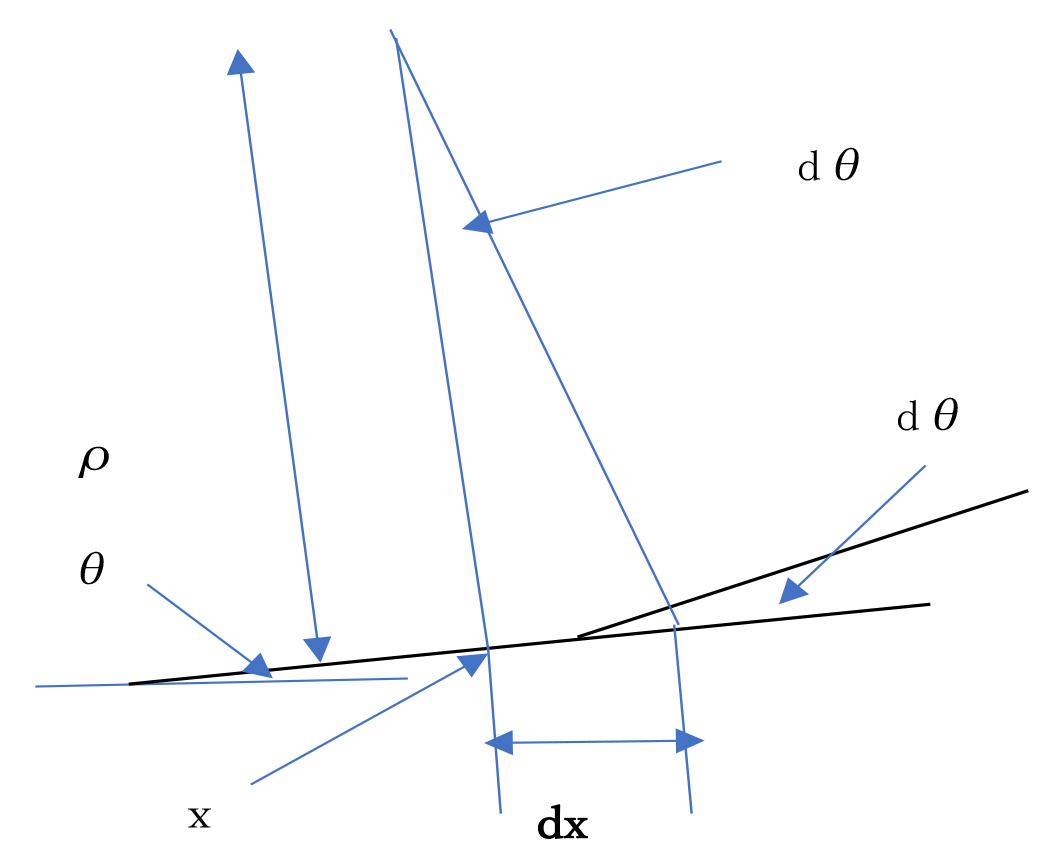
図‐３　　線の角度の変化と曲線半径

　一方、梁のように線に太さがある場合、断面の歪み分布の関係から上縁歪みεを上縁から中立軸までの距離a で除したε/a は、歪み勾配あるいは曲度(曲率)φと呼ばれ、この値は本稿の「その１」で示したように軸線の曲線半径ρの逆数に一致します。この関係を式〈２〉に示します。

φ= ε/ a = 1/ρ　　　　　 (2)

　すなわち、太さを持つ梁状の物体の曲がりの状態は、断面の歪み勾配が曲線半径の逆数に等しいとして式(2)として表されるのです。歪み勾配は断面の曲げモーメントMによって発生するのでこの関係はよく知られているように式(3)で示されます。ここで、aは上縁から中立軸までの距離、σ は縁応力度、Eはヤング係数、Iは断面2次モーメントです。これを変形して公知の式(4)が得られます。

σ = εE=(M / I ) a　　　　　 (3)
M /( EI) = ε/a = φ= 1/ρ　　 (4)

　太さを持たない純粋な線の曲がりに関して誘導した式(1)と、太さを持つ梁状の物体の曲がりの状態は、ともに曲線半径の逆数を表すので両式を一体とすれば曲げ変形に関する微分方程式である式(5)が得られるのです。ここで明らかなように「曲度」は線に太さを持たせた場合に必要な概念なのです。

d²y/dx² = M / (EI)　　　　　(5)

　曲線半径ρあるいは曲度φを一定として式(1)を解くと2次方程式が得られます。これが曲げモーメントが一定の場合の変位の式です。x =0およびx = Lでy = 0とすればその解は式(6)となります。

y = x (x -L) φ/2 　　　　　　 (6)

　単純梁を考え、支間中央の変位(撓み)δと支間Lとの比δ/L =qを撓み度とすれば曲度φが一定の場合、撓み度qは式(7)で表されます。

q= (1/8) φ L　　　　　 (7)

　式(7)でφを1/ρとすればq=(L/ρ)/8となり、撓み度は支間を曲線半径で除した値の1/8と表され興味深いです。さらに興味深いことに、この関係を円の直径を支間Lとして式(7)に適用してみますと、この場合の曲線半径はL/2ですので撓み度は1/4と計算されます。ところが実際には1/2であって明らかに誤った値です。この理由は式(7)の基本となる微分方程式が微小な曲がりの場合のみを対象としているからであって支間の1/2も撓む場合は適用外なのです。なお、撓み度が1/10の場合では真値との誤差が4%程度ですので実用上では式(7)は十分に精度の高い式です。

　道路橋示方書に規定される設計荷重が作用する場合には支間中央の曲度の値を用いるとすれば式(7)の係数は80%程度に低減されます。そこで、実用上では式(8)が有用となります。

q = 0.1 φ L　　　　　 　 (8)

　この式は、単純梁の支間中央の曲度が決まれば梁の撓み度が簡潔に求まることを示すもので曲度が一定ならば撓み度は支間長Lに比例するのであり、支間が大きくなれば無次元の撓み度が大きくなることになります。

　一方、式(8)を湾曲率ｗで表せばw = φ a なので式(9)になります。

　　　　　　　　　　　　　　　q = 0.1 w L/ a　　　　　 (9)

　大略の計算としてa を桁高 h の1/2 と仮定すれば支間桁高比（L/h）と撓み度qとの関係は式(10)で表されます。

q = 0.2 w (L / h)　　　　(10)

　例えば、支間桁高比( L/ h ) が20の場合、湾曲率が500×10 ^-6 であれば撓み度はq＝0.2x500x10 ^-6 x20 = 1 /500 となります。このように湾曲率が一定ならば撓み度は支間桁高比に比例するのです。

　PC桁の場合には一般に断面の上縁と中立軸の距離aは桁高h の0.4程度ですのでa=0.4hとすれば式(9)は式(11)となります。

　　　　　　　　　　　　　　　q = w (L / h)/4　　　　　 (11）

　湾曲率w は梁の上縁の歪みと同じ値ですので活荷重が作用した時の圧縮応力度をヤング係数で割れば容易に求められます。この値と桁高支間比を式(11)に代入すれば容易にPC単純桁の支間中央の撓み度が推定できます。

　湾曲率という構造工学上での概念はこれまでに存在しません。筆者の発案であり、英語では ”Rate of Curvature” あるいは “Non-dimensional Curvature”であると思います。太さを持つ梁状の物体の曲がりの状態を無次元で表現することは極めて有意義であり、曲がりの状態を普遍化できるのです。湾曲率の定義は、断面の平面保持が成立する梁状の物体において軸線の曲線半径の長さに対する断面方向の圧縮域の長さの比率であり、この値は圧縮縁の曲げ歪みに一致します。この比率が一定であれば梁状の物体は形象的に同一な相似形となります。この場合の圧縮縁の曲げ歪みは当然ながら同一の値となります。

　現在まで広く用いられている曲度（曲率、英語ではcurvature）は、数学や力学の分野における重要な事項ですが長さの逆数の次元を持つために梁状の物体の曲がりの状態を普遍的には表現できません。そこで、曲度に加えて新たに創出された無次元の湾曲率の概念を活用し、曲げ変形に関する対応をすることは意義のあることと考えられます。式(9), (10), (11) で示した撓み度と支間桁高比との関係が、湾曲率をパラメターとして明解に表現されていることもこの概念の意義を表している例であると考えられます。

　（１） 太さを持たない線は、論理的な概念上の存在であり、形象的には線は太さを持つと考えられます。線の曲がりの状態は曲線半径の大きさで一義的に定められます。　一方、曲度は線の角度の微分値であり、また、曲線半径の逆数であって長さの逆数の次元を持っており形として把握することは困難です。

　（２） 線に太さを持たせると、平面保持の仮定を用いることにより、無次元の湾曲率を定義することができます。これにより無次元で太さを持つ線の形状を定量的に定めることができるのです。

　（３） 梁の撓み度は、曲度あるいは湾曲率に比例する値として算定することができます。また、支間桁高比に湾曲率を乗ずることにより容易に撓み度を算定することができます。

　（４） 無次元である湾曲率は縁歪みと同値なので作用荷重の応力状態から容易に求められます。

　（５） 道路橋示方書の供用限界荷重が単純桁に作用する場合の撓み度は、この荷重によって支間中央部に生ずる縁応力度の値を用いることにより、支間桁高比の関数として式(９), (10), (11)により容易に概算値を算定することができます。
　撓み度は桁高支間比に比例するので当然のことながら桁高支間比が大きくスレンダーな桁ほど撓みやすいのです。