曲線半径の逆数、すなわち、「1/曲線半径」のことを「曲率」と今も称されていますが、無次元でないにも拘らず「率」という語尾を持つのは矛盾です。そこで「曲率」を「曲度」と呼び直してここでは表現します。「曲度」は次元を持つため、曲がりの程度を普遍的に表現できません。ここでは無次元の数字で曲がりの状態を普遍的に表すための「湾曲率」という新しい概念の提案に関し、その効用を述べます。湾曲率の基本に関しては本稿の「その2」をご参照ください。また、「曲線率」の概念を新たに加えました。

　曲線半径は曲線の曲がりの程度と形を定量的に表すことができます。曲線半径の逆数である曲度を用いる必要はないのです。また、曲度によって曲線の形状を把握しようと考えても曲度は通常の２次元平面での表現が不可能ですので無意味なことです。一方、梁のように線に太さがある場合の曲がりの状態は、梁の断面の歪み分布の状態によって表現できます。弾性体の場合には歪みは応力度に比例しますので断面に作用する曲げモーメントに起因して曲げ歪みが発生します。図-1 に示すように歪み分布の勾配が梁の曲げの状態を表現しているのです。

　図に示すように断面の上縁の歪みεを上縁から中立軸までの距離a で割ったε/a が歪み勾配でこれが本来の曲度Φです。図から明らかなように歪み勾配を構成する３角形は、曲線半径ρと中立軸での無次元の長さ1.0とで構成される三角形と相似ですので、歪み勾配はε/a = 1/ρであり、1/ρと一致するのです。したがって、梁のように太さを持つ線状の物体の曲げ形状は曲度によって表現するのが妥当なのです。

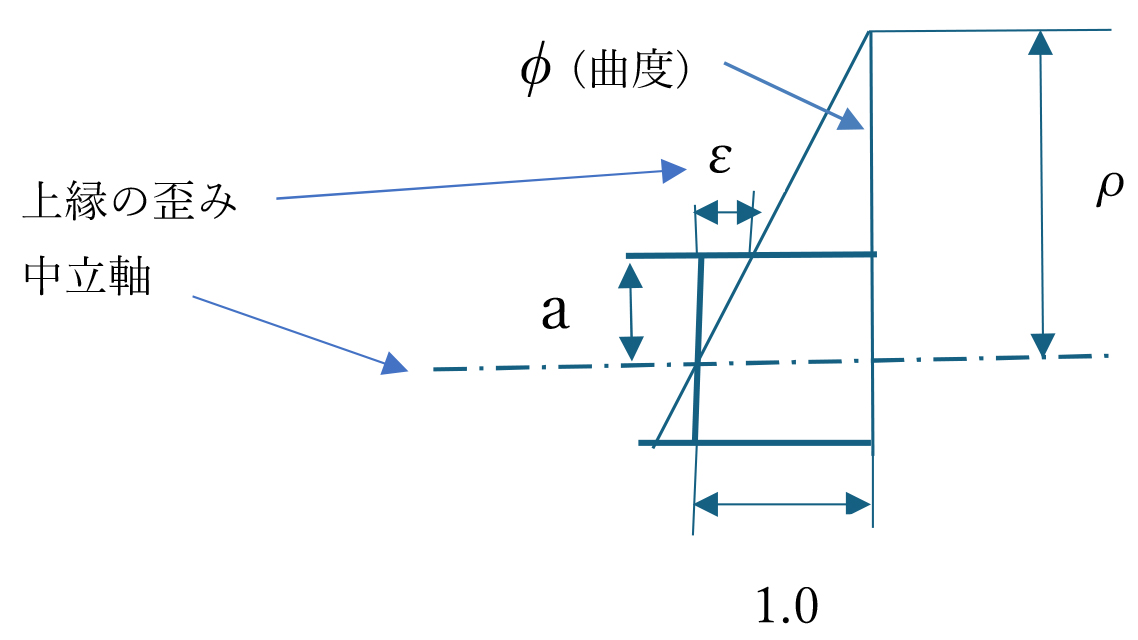
図-1　梁の歪み分布、曲度、曲線半径ρ

　図-1の横座標は無次元の座標軸であり、これに長さを掛けた場合は通常の平面における直交座標の横軸となり、歪み部分は変位、曲度部分は角度になります。すなわち、横軸が長さの次元では勾配は「角度」であり、横軸が無次元の場合は「曲度」であって名称的に「曲度」は妥当な命名と考えられます。本稿「その１」の図-2をご参照ください。

　曲度（＝曲率）を無次元的に表すために太さを持つ線を考え、その曲がり具合を普遍的に表すものが「湾曲率」です。図-1に示すように梁断面の外縁から梁の軸線（中立軸）までの距離をa とすればaと曲線半径 ρ との比率を湾曲率 w として　w = a/ρ = a φ と定義することにより無次元の表現ができます。ここで、φは曲度です。

　一方、曲度φは断面の歪み勾配なので図-1に示すように外縁の歪みを ε とすれば　φ＝ε/a です。これをwの式に代入すると湾曲率wは　w = εです。つまり、無次元の曲がりの状態として定義した湾曲率は、外縁歪みと全く同一の値なのです。あまりに簡潔なことなのですが極めて好都合です。湾曲率の概念は梁の撓み支間比（撓み度）を計算するときに極めて有用です。また、梁の曲がりの状態を無次元で普遍的に表すことができるのです。

　単純梁を考え、支間中央の変位(撓み)δと支間Lとの比δ/L =qを撓み度（撓み支間比）とすれば曲度φが一定の場合、撓み度qは式(1)（本稿「その２」の式(7)）で表されます。

q= (1/8) φ L 　　　　　(1)

　道路橋示方書に規定される設計荷重が作用する場合には支間中央の曲度の値を用いるとすれば式(1)の係数は80%程度になると仮定できます。そこで、近似的には式(2)となります。

q = 0.1 φ L 　　　　　　 (2)

　この式は、単純梁の支間中央の曲度が決まれば梁の撓み度が簡潔に求まることを示すもので撓み度は支間長Lと曲度に比例するのであり、曲度が同じなら支間が大きくなれば無次元の撓み度が大きくなることになり不都合です。なぜなら曲度は次元を持つからです。

　一方、式(2)を湾曲率ｗで表せばw = φ a なので撓み度は式(3)になります。

q = 0.1 w L / a　　　　　 (3)

　湾曲率の導入により撓み度と支間桁高比との関係が定まります。一般的な計算としてa を桁高 h の1/2 と仮定すれば支間桁高比（L/h）と撓み度qとの関係は式(4)で表されます。

q = 0.2 w (L / h)　　　　 (4)

　例えば、支間桁高比( L/ h ) が20の場合、湾曲率が500×10^-6 であれば撓み度はq＝0.2x500x10 ^-6 x20 = 1 /500 となります。このように湾曲率が一定ならば撓み度は支間桁高比に比例することが解ります。

　PC桁の場合には一般に断面の上縁と中立軸の距離aは桁高h の0.4程度ですのでa=0.4hとすれば、w L/a=w L /(0.4h)=2.5w(L/h)なので式(3)は式(5)となります。

q = 0.25w (L / h) 　　　　(5)

　湾曲率w は梁の上縁の歪みεと同じ値ですので活荷重が作用した時の圧縮応力度をヤング係数で割れば容易に求められます。この値と支間桁高比を式(5)に代入すれば容易に道路橋示方書の設計活荷重が作用した時のPC単純桁の支間中央の撓み度の概略値が求められます。

　表-1に支間桁高比(L/h)を縦、撓み度(q)を横列とした場合の式(5)で求まるPC桁の湾曲率の値を示します。例えば支間桁高比(L/h)が20の場合、撓み度(q)が1/1000のときには湾曲率(w)は200×10^-6です。湾曲率は上縁の歪みの値と同じですからこれにヤング係数を掛けると上縁の圧縮応力度の値となります。ヤング係数を30GPaとすれば上縁の圧縮応力度は6MPaとなります。湾曲率は活荷重による支間中央の曲げモーメントによって定まりますので、この表から支間中央の湾曲率に対応する支間桁高比と撓み度の関係を容易に把握することができます。

表-1　支間桁高比(L/h)と撓み度(q)に対応する湾曲率(w)の値 (x10^-6)

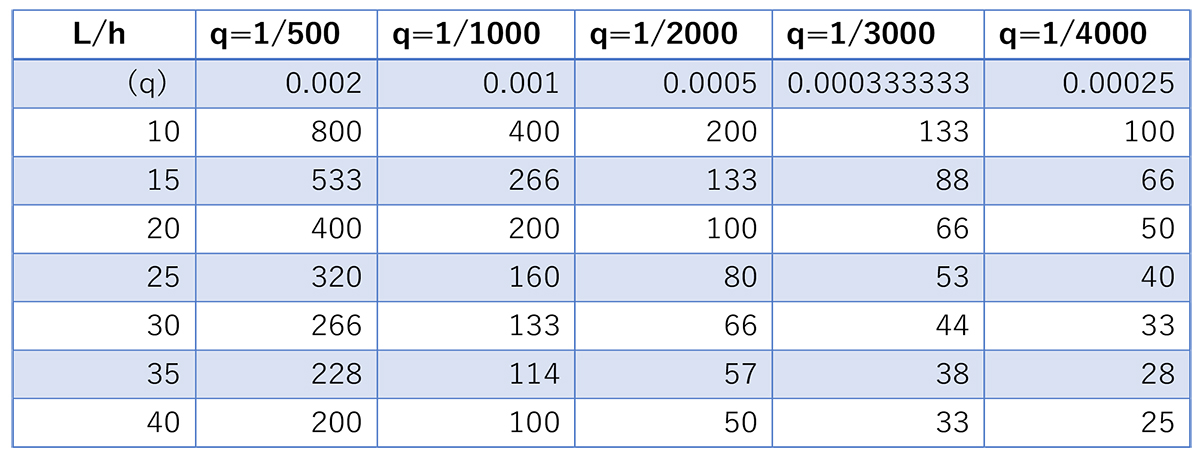
表-2 支間桁高比(L/h)と撓み度(q)に対応する上縁応力度 (MPa)

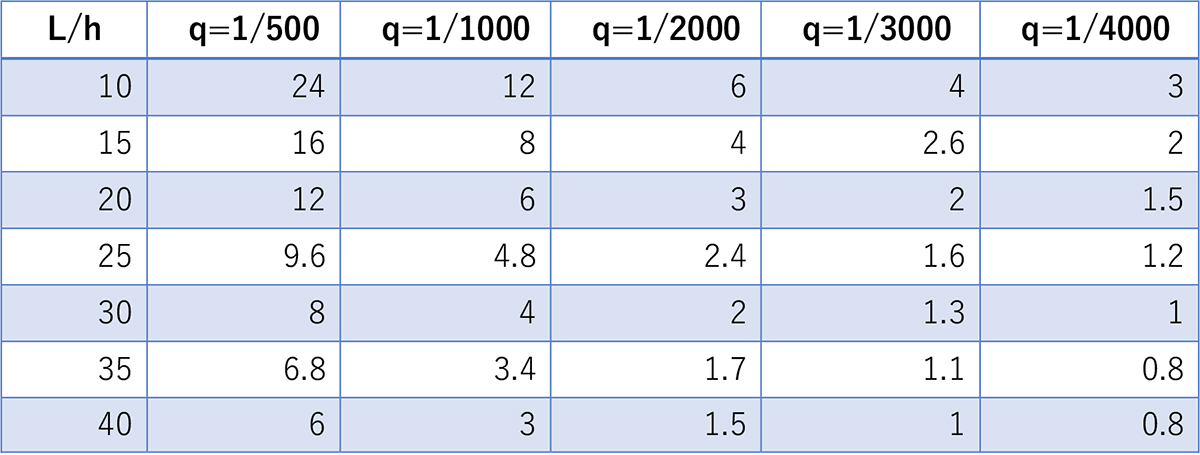
　表-2にヤング係数を30GPaとした場合の湾曲率に対応した上縁の応力度の値を示しました。前述のようにL/hが20, qが1/1000 の時には上縁の応力度は6MPaです。

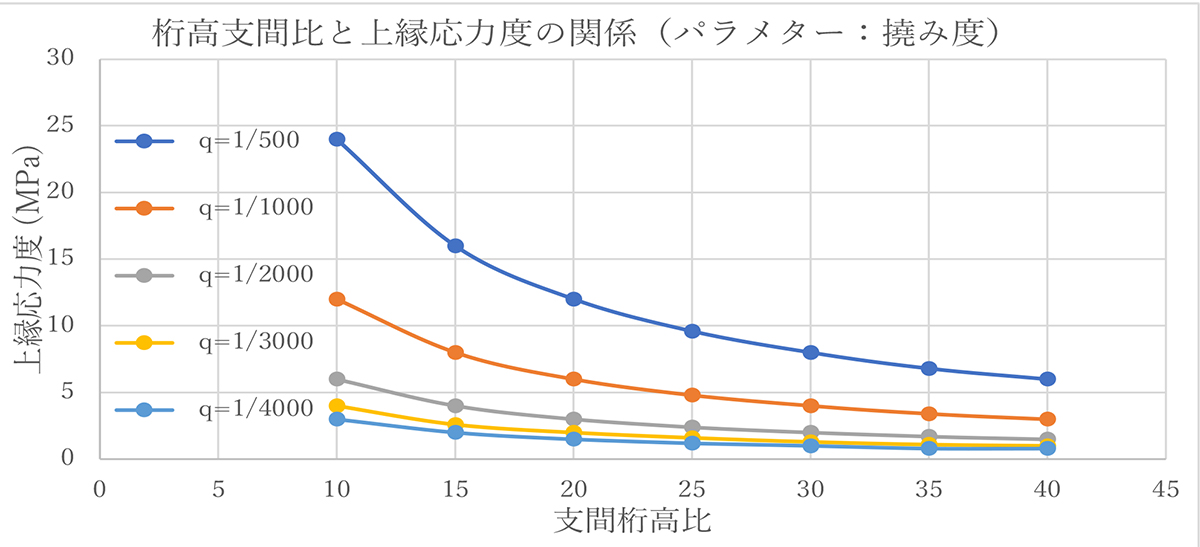
図-2　撓み度をパラメターとした支間桁高比と上縁応力度の関係

　図-2に撓み度をパラメターとした支間桁高比と上縁応力度の関係を示します。この図は表-2 を図化したもので設計上、撓み度を検討する必要がある場合に支間桁高比による影響を視覚的に把握するのに有用と思われます。図-3には上縁応力度と支間撓み比の関係を示します。ここでは撓み度の値は小さいことと、通常は1/500 あるいは1/1000 のように分数で表現されますので、縦軸には支間撓み比として撓み度の逆数を表示しました。

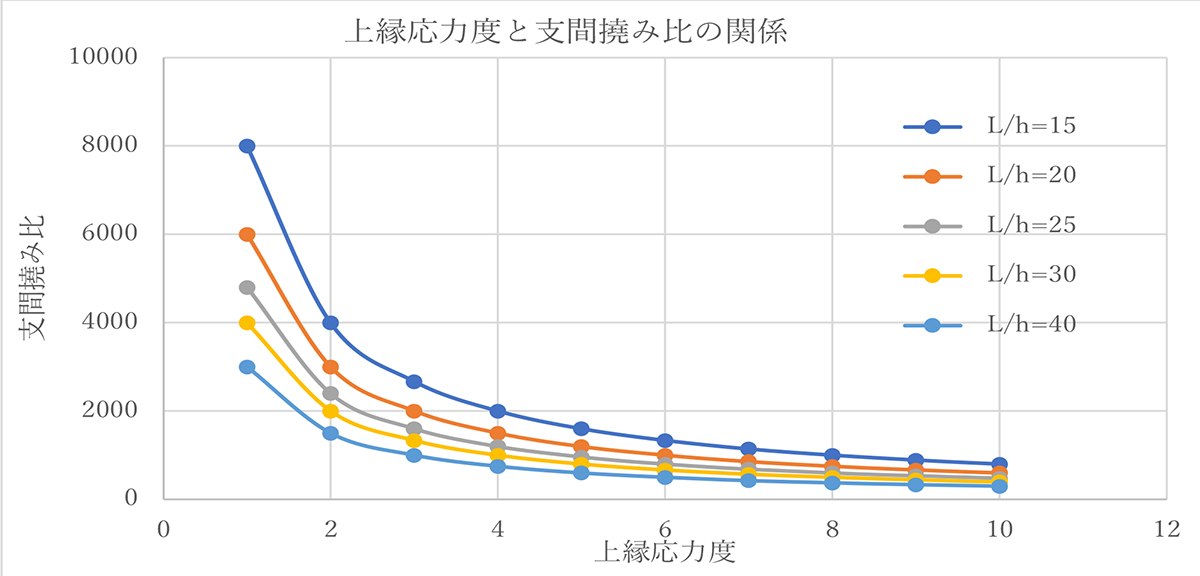
図-3　上縁応力度と支間撓み比（撓み度の逆数）の関係