床版などの実験報告は6.2で述べたような結果報告が一般的である。これは床版などの実験は費用も大きくなり、実験の際の苦労が多いためであり、示方書で設計した供試体に設計荷重の２倍程度の荷重Pで実験して、その破壊寿命、あるいは載荷回数をNpとして、設計荷重を載荷した場合の破壊回数NdはS-N[曲線の傾きの逆数の絶対値mを仮定する。例えば、Nd＝Np×(P/Pd)^ｍを求めて、設計寿命中で設計荷重相当の載荷頻度はこの回数のNdより十分小さいので、この構造物は疲労に対して安全である等の考察で結論としていたようである。

　上記の成果を理屈に合ったものにするには多数の実験を行い、合理的なS-N図を求める必要がある。筆者はたまたま良いスポンサーがついてくれたことと、継続的に多くのすぐれた献身的な学生の手助けもあって多くの実験ができ、上記のS-N図の作成ができたのである。以下、合理的なS-N図作成の経緯を披露したい。

 

　6.3.1　コンクリート構造物の疲労強度は「載荷荷重／部材の耐荷力」の無次化量を縦軸にするが？

　構造物の疲労強度あるいは疲労耐久性の表現は、鋼構造のようにある部位のひずみ、あるいは応力とそれらの発生頻度との関係で表されるが、コンクリート構造物は荷重を受けると、一般的にコンクリートにひびわれが発生し、非線形で、かつ不均質な応力状態となり、疲労耐久性は一つの着目点の応力等では説明できない。例えば、鉄筋コンクリート梁の曲げ試験をする場合、材料的に均質な鉄筋にゲージを張り付けて荷重とひずみの分布状態の変動を見た場合、ひずみは曲げモーメントのようにスムーズな連続分布で変化はしない。分布はコンクリートに発生しているひびわれ（ひびわれ間では力の伝達が無くなる）の影響を受けてスムーズな分布を示さなくなる。

　このような特性から、コンクリート構造物の耐久性評価は、「載荷荷重／その構造物の耐荷力」の無次元量と載荷頻度との関係をS-N相当図で表現されてきたようである。

　この手法を用いて道路橋RC床版のS-N図を作成する研究を続けてきた。大きな障壁は、RC床版では、最終破壊は載荷直下で複数本の鉄筋が降伏して大きなたわみを伴う曲げ破壊ではなく、たわみは最大でも3cm程度の内に、突然載荷板が陥没する押抜きせん断破壊する、ことである。静的載荷で走行載荷でも同様であると分かったので、S-N図の縦軸は載荷荷重をその床版の押抜きせん断破壊強度で無次元化を行うのが当然と考えた。そして、疲労実験する場合には必ず2体同時に作成し、1体は疲労実験供試体として、もう1体を静的に破壊させ押抜きせん断耐力用にすべきであると考えたが、これは到底無理な話であると考え、精度の良い実験式が無いかと文献調査し、発見すると私の実験データと代入して実験値との対応を自身で調べた。しかし、良い結果は得られなかった。


 

6.3.2　角田式の発見

　諦めかけていた時、北大の角田與史雄教授の論文を発見した。角田先生も目的は異なるが、私と同様な考えを持っておられて、ご自分でパラメーターを変化させて60体強の供試体を作成し押抜きせん断破壊実験を実施され、四人の外国研究者が提案されていた経験耐荷力式と実験値との対応を、ご自身が提案された式（１）との対応との比較で示されていたのである。比較の結果を図6.7に示したように角田先生の推定精度は群を抜いて良いものであった。

 

図6.7　角田式　と（角田教授らの実験値／各研究者提案の推定式）の適合性比較

　この論文では全供試体の必要パラメーターも掲載されていたので私はバイブルの如く持ち歩き、過去の実験値との比較を行ったのである。ここに、私が発見した結果を述べたい。

 

6.3.3　角田式の道路橋床版への適用性

　角田教授が精度の良い推定式が提案されたので、この式を私の実験データを含めて、道路橋床版と銘打った実験値との対応を調べた。その結果は図6.8に示したように、図6.7e）よりもバラツキは大きくなった。

　非常に悩んだ末、分かったことは、道路橋床版として実験された事例では、全てが長方形載荷板上に荷重が載荷されていた。一方、角田並びに諸外国の研究者は円形載荷板、あるいは正方形板上に載荷していたのである。これらの研究者らは床版を柱で結合した、所謂建築の床などの柱間隔の大きいスラブと柱結合部における配筋を研究対象にしていたと言える。配筋が悪い場合やスラブの厚さと柱間隔Kが大きい場合には、柱に作用する力が大きくなって結合部で押抜き破壊が生じる。このような事故対策を確定するため、スラブの押抜き破壊問題を取り上げ、スラブだけの実験を正方形や円形の載荷面で実験したのである。

　角田教授は土木科の先生であるので、建築の床や天井の研究はしていないと思われるが定かではない。

図6.8　道路橋床版として実験された結果に角田式を適用した結果

　道路橋床版としてもちいる場合には、荷重は大型トラックの後輪荷重に対しての抵抗性を調べるため、ほとんどの研究ではダブルタイヤの接地面をモデル化した接地幅50cm×接地長20cmの長方形の接地面上に載荷しなければならない。もし、供試体を小さくしても載荷板は縮小しても形状は長方形でなければならない。

　角田教授が提示された耐荷力式(１)に鉄筋の降伏応力σsyがパラメーターの一つとして入っているが、私の実験経験では鉄筋は降伏する前にコンクリートだけが押抜き破壊しているようであった。この気付き後、私は実験において破壊近くなると、必ず床版の下にもぐり、破壊時のひびわれ方を観察する習慣がついた。

　余談になるが、実験の時、周りの学生や同僚は危険ですから早く出てこいと叫ばれるのだが、下に居る方が安全だと答えている。上にいる方が、ジャッキが落下したり、ロードセルが飛んだりして危険が大きいのである。

 

6.3.4　道路橋床版の押抜きせん断耐荷力式　－松井式―

　　RC床版に長方形載荷版を用いて荷重かけると、曲げ変形のためたわみが増大するが、途中で大きな音と共に、床版が押し抜かれて荷重が低下するので載荷を停止する。破壊部を観察すると，上面では載荷版部が綺麗な長方形状に陥没し、その陥没位置から下方に45度の角度で斜め方向にひびわれ、明瞭にせん断破壊したと判る。下面では、引張側鉄筋がせん断力の一部に対して抵抗するので（このせん断力はダウエル力と名付けられるもので、45度のせん断ひびわれと下側鉄筋との交点で鉄筋に対して鉛直力が作用する。編注参考）この力によって、下側鉄筋に沿ってコンクリートが割裂される。この割裂長さはかぶりコンクリート厚の2倍から4倍位に見える。この陥没した部分のコンクリートを丁寧にはつり落とすと、鉄筋は上記ダウエル力の作用位置で曲がりが若干大きいが、降伏したような感じはしない。

　この観察結果を図示し、床版内の抵抗状態を併記したものが、図3.8である。

図3.8　長方形載荷板による走試験破壊時のひびわれ状態と、所々の発生応力分布のモデル化

　この図は、作用荷重と載荷板回りの発生応力との釣り合いが最も適合するのが、被りコンクリートの割裂長さを主鉄筋、配力鉄筋のかぶり厚さの2倍にしたものである。a)図に示した破壊時の主鉄筋に直角断面に作用している応力分布であるが、配力鉄筋に直角の断面に作用している応力状態も同様と考えて、これらの応力の鉛直成分の平面分布をb)に示した。

新たに考えだした松井式　

　載荷板下の圧縮側のせん断応力は等分布するので、鉛直成分は単純にこの応力値に中立軸深さを掛け算し、作用位置を載荷板から被り深さ離れた位置にした。数学的には中立軸深さの1/2離れた位置にすべきであるが、表現を簡単にした。中立軸深さは小さいので誤差は僅かである。また、かぶり部の割裂長さは、前記したようにかぶり深さの2倍とし、割裂の引張力は三角形分布していると考えた。この割裂破壊部の四コーナーでは円形状に分布させるべきであるが、主鉄筋および配力鉄筋のかぶり厚さが異なるので、本来楕円形に近い分布形状となると思われるが、これも簡単に深さを主鉄筋のものを使用し、長方形状に分布するように表現を簡単化し、最終的に式（３）の代数式で表すことができた。この式は全てがコンクリートの強度と幾何学的寸法だけで表現できたわけである。この式を用いて図6.8の道路橋床版の実験値と計算値の比の適合状態を示したのが図6.9となり、図6.8と比較し飛躍的に一致度が向上したと言える。

　この式を用いて、角田教授が行った60体強の供試体の実験値と計算値の比を頻度図で表したものが図6.10であるが、角田教授が示した頻度図に勝るとも劣らない整合性で、式（２）が正方形板で載荷した床版の押抜き強度も推定できることが明らかになった。

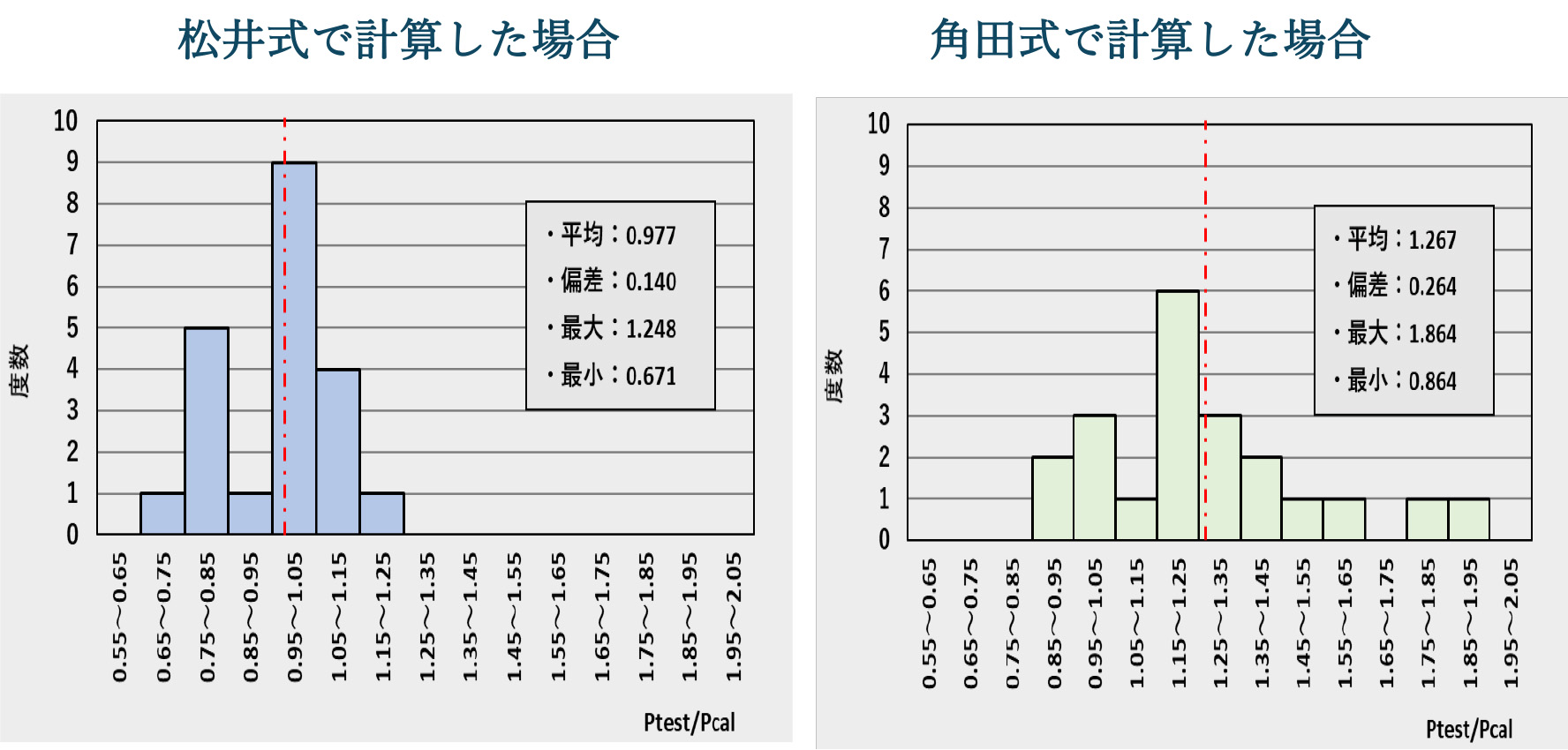
図6.9　長方形板用いた道路橋床版の松井式と実験値の対応（前出の図6.8との比較）

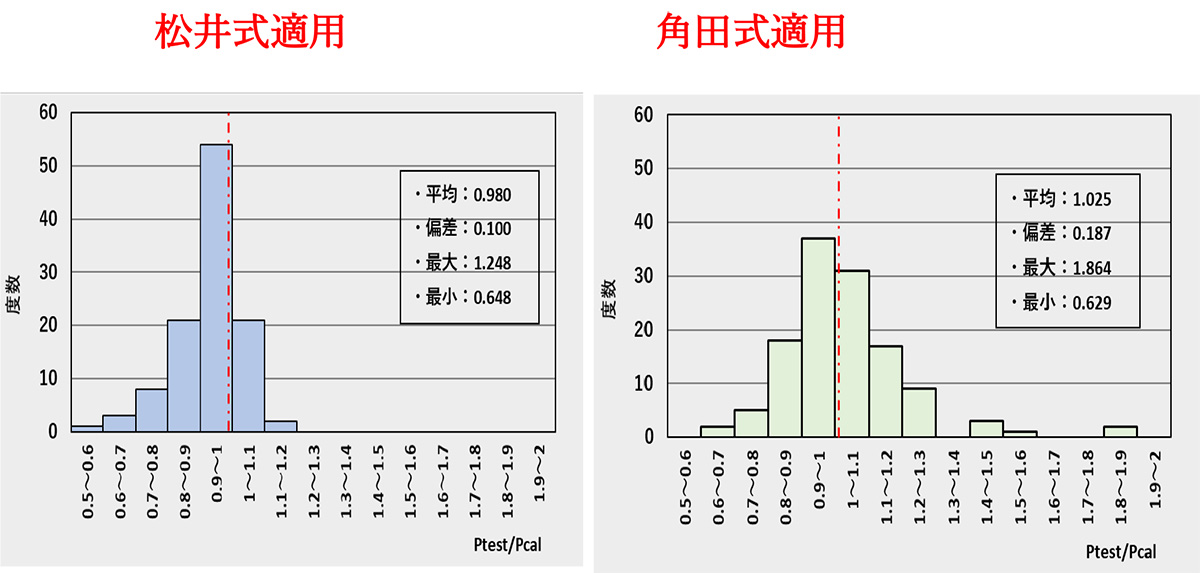
図6.10　角田教授が実験した正方形載荷板による床版に対する松井式の適用性の検証結果

　上記6.3.3と6.3.4の全照査計算をチンチンジャラジャラのタイガー計算機を回して、3日間でできたので、嬉しさで興奮して、若干の睡眠しかとれなかったが、この結果を４日間で土木学会論文集への投稿論文に仕上げた。本論文は私の最も誇りとするものである。

 

6.3.5　出来たS-N曲線は定点疲労試験の約80～100倍速く破壊することが判った！

　飛躍的に一致性が向上した押抜き耐荷力式で走行実験を実施した全供試体の押抜きせん断耐力を求めPoとし、これによって無次元化した値を縦軸にとり、その各床版の破壊寿命を横軸にとってS-N図にプロットした。この結果は図6.11で明らかなように適用示方書毎に直線分布した。この図に園田教授が行った6cm厚の床版の結果もプロットした。

　設計要領毎の直線で分類されるが、各ケースとも松井の大型試験体の傾きと同じになった。やはり押し抜きせん断耐力式の精度が上がったためと思われる。このようにS-N曲線が直線で表すことができたので、RC床版の疲労設計ならびに既存床版の疲労耐久性の評価が可能になったと言える。

図6.11 　走行する輪荷重を受ける床版の疲労強度曲線

　この図に、定点載荷による疲労実験結果を5,6本の直線で併記したが、輪荷重が走行することによってこれらの定点載荷による疲労強度を大幅に下回ることとなった。この図中に、例としてS＝0.5の所で、大きな星印で走行試験の場合（赤星）と定点載荷の場合(黒星)との疲労寿命差が簡単に判る。定点載荷の黒星では平均寿命は約500万回となるが、走行載荷では僅か500回で破壊こととなり、この1万倍の疲労寿命差が輪荷重が走行するか固定するかの差であり、走行することの凄さであると理解して貰いたい。道路橋の床版は大変過酷な荷重作用を受けているのである。

図6.12　一つのひびわれを含む床版要素に作用する断面力とひびわれの動き

図6.13　車輪の移動毎にずれ挙動が発生し配力鉄筋断面が貫通ひびわれに成長

　上記の疲労の速度差は、図6.12に示した床版要素を見た場合、ひびわれに平行面に作用する曲げモーメントによる開閉の繰り返しと、鉛直方向のせん断力による鉛直方向のズレ、ならびにねじりモーメントによる水平方向のズレが発生する。開閉でひびわれ面の劣化は無いが、ズレがひびわれ面の損傷の原因となる。道路橋では車輪の進行方向に直角断面、すなわち配力鉄筋に直角断面のせん断力は車の移動毎に交番繰り返しが起り、容易に配力鉄筋に直角が貫通するひびわれが発生する。定点載荷の場合でも、せん断応力の集中は発生するが移動しないので振幅は半分程度あり、同一方向であるのでひび割れ面のこすり合わせは非常に少ない。この点が明らかに相関している。よって、図6.11のS-N図での1万倍の疲労寿命差は、走行荷重でせん断力が交番することにあると説明できる。

　図6.11のS-N図を描くために荷重をその床版の押抜き耐荷力Poで無次元化したことで気付いた点がある。大変重要なことである。

　すなわち、図6.11の各S-N曲線が平行になった点である。各平行線の高さ方向の差は当然強度差であろうが、Poの計算で反映されているので、別の要因があり一本のS-N曲線で表わせないのは無次元化の分母が悪いのではと考えた。それで走行試験で破壊するのは載荷板の全周ではなく、主鉄筋断面だけではないかと気付いた。すなわち、走行荷重を受けた床版は、40～50cm幅間隔で貫通ひびわれが発生し、ひびわれ面の磨耗が進んで、はり状化した梁が過大せん断力を受けて、その梁の主鉄筋断面がせん断破壊すると実験結果を纏めていたことを忘れていたのである。

　それで、はり状化幅の40～50cmの幅をより合理的に表せないかと考えたが、最終的に、載荷板の橋軸方向の接地長20㎝にその床版の配力鉄筋の有効高さの2倍（載荷板の前方と後方分）とすればほぼ満足と考えた。後日、薗田先生の後輩で床版研究されていた堀川都志雄大阪工業大学教授が床版解析から、梁幅は床版の輪荷重作用時の有効幅程度であり、私が考えた上記の幅とほぼ一致すると教えて頂いた。

　それで自信をもって、図6.14に示すような梁幅で抵抗し、この梁幅で圧縮側のせん断応力と引張側位置での割裂応力がそれぞれの限界値に達した時に主鉄筋断面が破壊するとしたはりのせん断破壊強度Psxをもとめ、これで載荷荷重を無次元化した縦軸でS-Nデータをプロットしたものが図6.15である。

　全データは一本の直線の周りにプロットできた、これらの中央線が統一化されたS-N曲線で、RC床版の疲労設計や耐久性評価に十分耐えられるものと思っている。

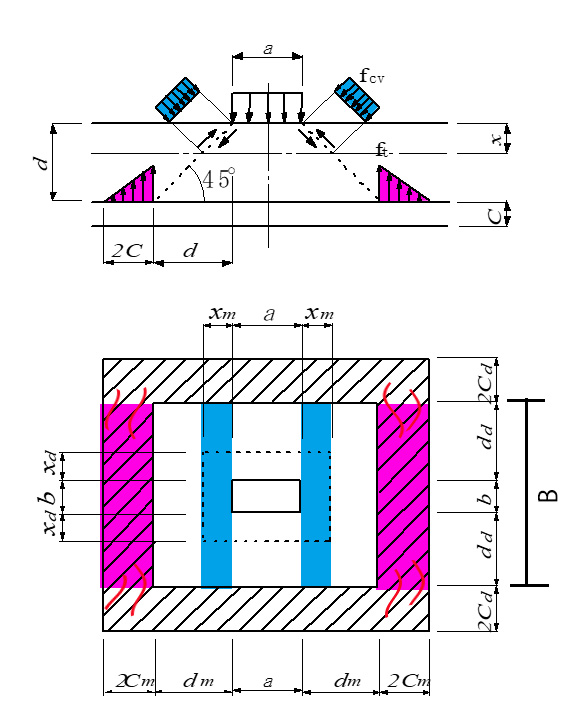
図6.14　はり状化幅（b＋２dd）で、上部のせん断応力と下側かぶり部の割裂応力の総和でPsxを表現できる
すなわち、　Psx＝２･B（fcv･Xm＋ft･Cm）　となる。

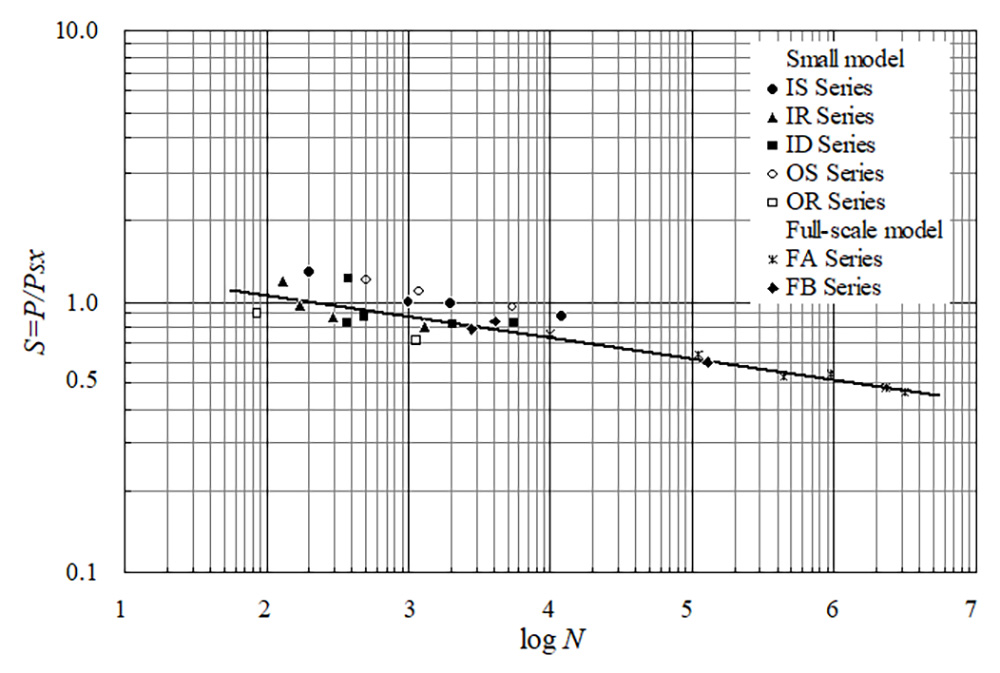
図6.15　縦軸をP/Psxで無次元化した全S-NデータによるS-N曲線
【 log(P/Psx) = -0.07835･log N + log 1.520 】

　次は水の影響と高耐久性床版の話題について記す。【次回は3月1日に掲載予定です】